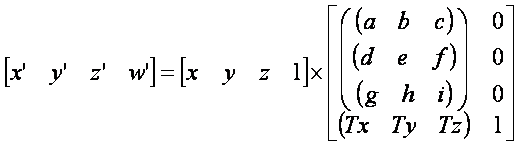
PS2 Linux Programming
Understanding The World Matrix
Introduction
Controlling the movement of objects in 2 and 3 dimensions stems from an understanding of the world transformation matrix. In this tutorial the component parts of the world transformation matrix will be investigated and the world transformation matrix will be used to move and manipulate a sprite in three dimensions.
The world transformation matrix used for three dimensional graphics is a 4x4 matrix of the form shown below.
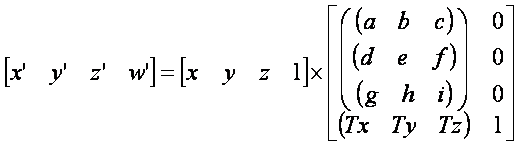
This matrix is used to position and orientate an object in world space. To put this another way, the world transformation matrix transforms the coordinates of the model from local (or model) space to world space.
As can be seen from the matrix layout given above, the world matrix can be considered to be constructed from three parts, a 3x3 matrix:
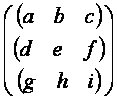
which is mainly associated with the orientation or rotation of the object, a 1x3 matrix:
![]()
which is associated with the position of the object in world space, and a right hand column which is always (0001) under normal circumstances.
The translational part is relatively straightforward, it positions the model in the world at coordinates (Tx, Ty, Tz).
For the purposes of this discussion, the 3x3 matrix part of the world matrix will be considered to be a pure rotation matrix. A pure rotation matrix has some very special properties and in mathematics it is called an orthogonal matrix. An orthogonal matrix (A) has some interesting properties which are very useful for use in computer graphics and games programming. Some of the properties of an orthogonal matrix are:
1. Multiplying an orthogonal matrix by itís transpose gives the identity matrix.
![]()
2. The length of the vector produced from each row (or column) of an orthogonal matrix is unity or 1.
3. The directions of the vectors that represent the rows of an orthogonal matrix are all mutually perpendicular.
4. The rows of an orthogonal matrix represent the unit (or directional) vectors of the axes of the object when placed in world space.
Properties 1, 2 and 3 are useful for verifying that a matrix is a rotation matrix but it is property 4 that is of most use to games programmers. Property 4 is useful for forward motion. If the object is moved in the direction of the vector defined by the first row of the matrix then the object will move in the direction that itís local x axis is pointing. If the object is moved in the direction of the vector defined by the second row of the matrix then the object will move in the direction that itís local y axis is pointing. If the object is moved in the direction of the vector defined by the third row of the matrix then the object will move in the direction that itís local z axis is pointing.
Now, suppose that in the writing of a game, an object is situated in a 3D world and is facing some random direction, and the object must be moved straight ahead in the direction it is pointing (such as controlling the movement of a car in a racing game, or the motion of an aeroplane in a flight simulator), then how is this done? The answer lies in the rows of the rotation matrix. To move the object in the direction that itís x axis is pointing, a factor (n) of the first row of the rotation matrix is added to the translation part of the world matrix as illustrated below.
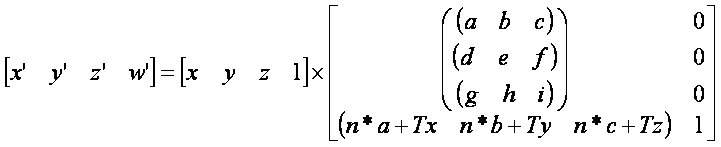
That is all there is to it! There is no need to calculate angles or even know what they are Ė everything that needs to be known is contained in the world matrix. It is possible to move forward/backwards by simply applying the above relationship. Similarly, in order to move to the right or left (strafe or y-axis) the values in the second row can be used and to move up or down (z axis) the values in the third row can be used.
The code in the project accompanying this tutorial illustrated the techniques introduced above. Even although the sprite is a flat textured quad, all of the movement characteristics found in 3D games can be demonstrated and observed. The function to move the sprite in the direction of itís local axis is:
//move sprite in the direction it is pointing
void MoveSprite(PS2Sprite_t * pSP, float Delta, int Axis)
{
// This moves the sprite along its local "Axis" axis
// by an amount Delta
pSP->Pos.x += pSP->World(Axis,0) * Delta;
pSP->Pos.y += pSP->World(Axis,1) * Delta;
pSP->Pos.z += pSP->World(Axis,2) * Delta;
}
The axis of motion (Axis) is passed into the function this being either 0, 1, or 2. A pointer to the sprite to be manipulated is also passed along with the factor (Delta) by which the sprite is to be advanced. It can be seen that the position vector of the sprite is updated by the appropriately selected vector.
Within the sprite structure there are variables RotX, RotY and RotZ to hold the rotation angle of the sprite round all of the three axes. In the function BuildSprite2D() methods RotationX(), RotationY() and RotationZ() are used to build a rotation matrix from the three rotation angles. Once the translation components of the sprite are added, this matrix is applied to the untransformed coordinates of the sprite to generate the positions of all four vertices of the sprite in world space. The GS packet is constructed from this vertex data as in previous tutorials.
On running the program the sprite is drawn on screen as an animated character which walks around the screen under control of the user. The rotation of the sprite is controlled with the left hand side of the controller: left and right control rotation round the local z axis, up and down control rotation round the local y axis and L1 and L2 control rotation round the local x axis. The translation of the sprite is controlled with the right hand half of the controller: the circle and square control movement in the local x axis, the triangle and cross control movement in the local y axis and R1 and R2 control movement in the local z axis.
This tutorial has outlined the significant properties of the world transformation matrix which are important to the programming of computer games. It has been shown how the world transformation matrix can be used to control object movement within both 2 and 3 dimensional computer games.
Dr Henry S Fortuna
University of Abertay Dundee